Viscoelastic Models for Linear Viscoelastic Response

Most polymers do not exhibit viscoelastic behavior described by the simple Maxwell and Kelvin models because the conformational changes and the viscous flow are constrained by a multitude of physical entanglements and chemical crosslinks which impair viscoelastic flow in a very complicated way. The situation is further complicated if the polymer in question has a complex morphology such as crystalline domains dispersed in an amorphous matrix, microphase separated polymer domains and interpenetrated polymer networks. For these materials, more elaborate spring-dashpot models have to be employed to effectively describe their complicated viscoelastic behavior.

The simplest model that captures both the relaxation and retardation is the so-called standard linear solid model (SLS Model), also known as the three-parameter model.1,2 This model is obtained by adding a spring either in series to a Voigt model or in parallel to a Maxwell model (see Figure a) and b) below). This model is sometimes referred to as the Zener Model3 and is employed to describe a material that will fully recover after a load is removed because the spring connected in parallel to the Maxwell element will continue to move the piston of the dashpot back to its original position. Thus, Zener models represent solids that undergo a reversible deformation. i.e. they describe a rubbery material.

  

Standard Linear Solid Models3

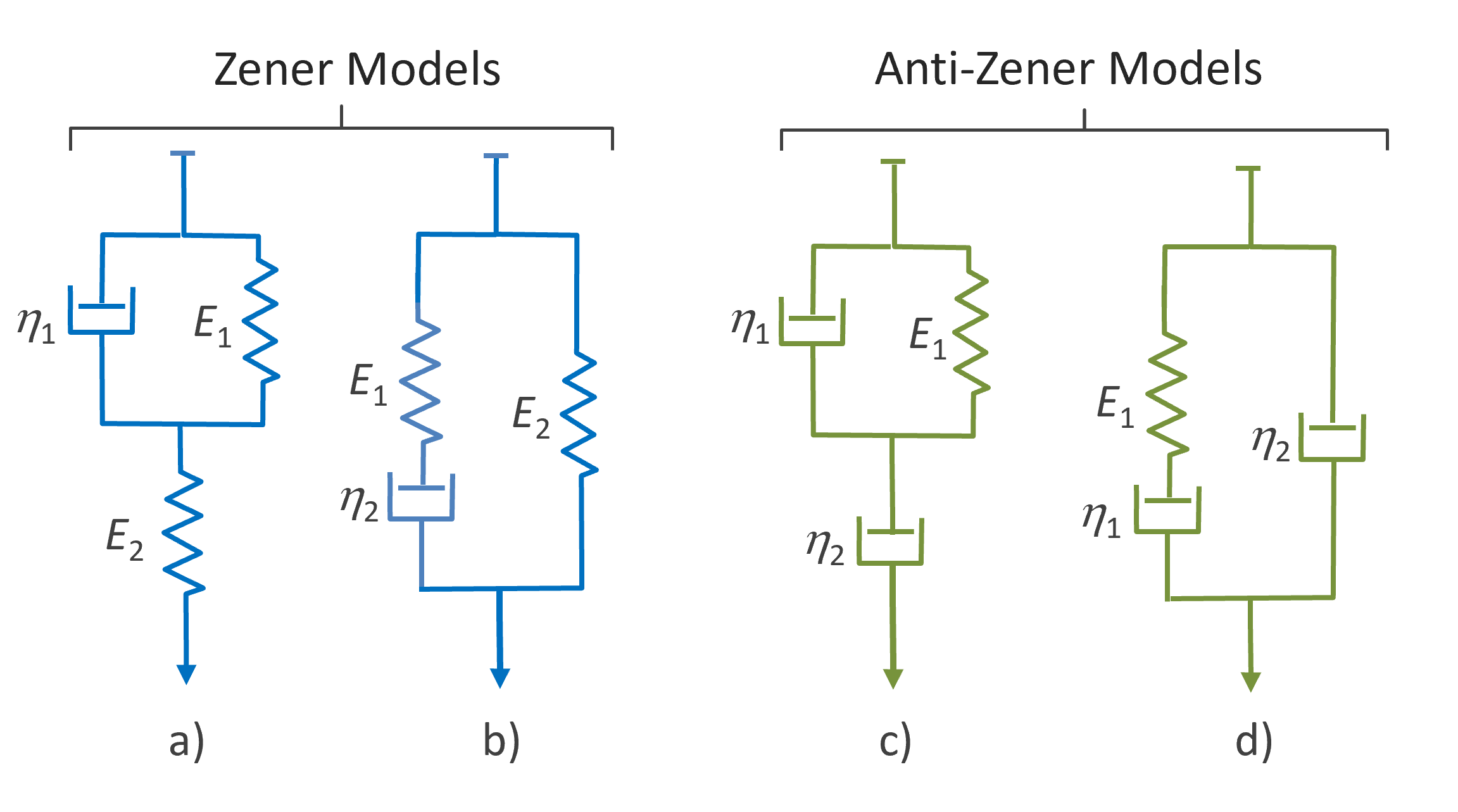
The simplest way to describe a solid that undergoes both permanent and elastic deformation under stress is an arrangement of a dashpot either in series to a Voigt (Kelvin) model or in parallel to a Maxwell model (see Figure c) and d), respectively). These models are sometimes referred to as anti-Zener models.3 They describe a material that will only partially recover after a load is removed because the piston of the dashpot connected in series to the Voigt element will not move back to its original position when the load is removed. Thus, anti-Zener models represent a solid that undergoes both a permanent and elastic deformation which is the typical behavior of a thermoplast.

The three-parameter model can be easily solved if we make use of the solutions of the Voigt and Maxwell elements. For example, the creep in the Zener arrangement a) is the sum of the strain in the Voigt model and in the spring:

ε = ε1 + ε2
ε1 = σ0 / E1 · [1 - σ0 e-t/τ],   ε2 = σ0 / E2

Then

ε(t) = σ0 / E1 · [1 - σ0 e- t/τ] + σ0 / E2

where ε1 is the (time-dependent) strain of the Voigt model, ε2 is the strain of the spring and τ = η1/E1 is the response time of the one-dimensional Voigt element. The strain rate (creep rate) is given by its derivative

dε / dt = σ0 / η1 · e- t/τ

The strain equation of the Zener model has three unknowns which can be determined from the creep curve and from following initial conditions at t = 0:

ε1 = 0;    ε2 = σ0 / E1
and
dε / dt|0= σ0 / η1 = tan α

where tan α is the initial slope at t = 0. In many cases, the initial strain rate is so large that α is close to 90°.4 Then η1 can not be determined directly.
According to the Zener model, an instantaneous stress causes only the spring 2 to initially expand, while the Voigt element only slowly and gradually deforms. Thus, for times much shorter than the relaxation time, τ, the Maxwell element behaves essentially like a spring, whereas for times much longer than the relaxation time, it behaves like a dashpot.

While some problems in viscoelasticity can be solved with three-parameter models, more often Voigt and Maxwell elements are combined to more complex arrangements. One very popular model is the so-called four-element model, also known as the Burgers model. It consists of a Maxwell element and a Voigt element in series. The Figure below shows this model and its creep and recovery curve. It is the simplest model that exhibits all the important features of viscoelasticity: on application of a stress, σ0, the model experiences an elastic deformation, followed by creep that leads to a permannent deformation (true flow). The recovery curve is also shown in the Figure below. It consists of an instantaneous elastic recovery, followed by a creep recovery at a decreasing rate and with permanent deformation which is solely determined by the first dashpot. In other words, after removal of the stress, the model only partially recovers from the deformation which is the common case for a thermoplastic material.

  

Creep and Relaxation Behavior of Burgers Model4

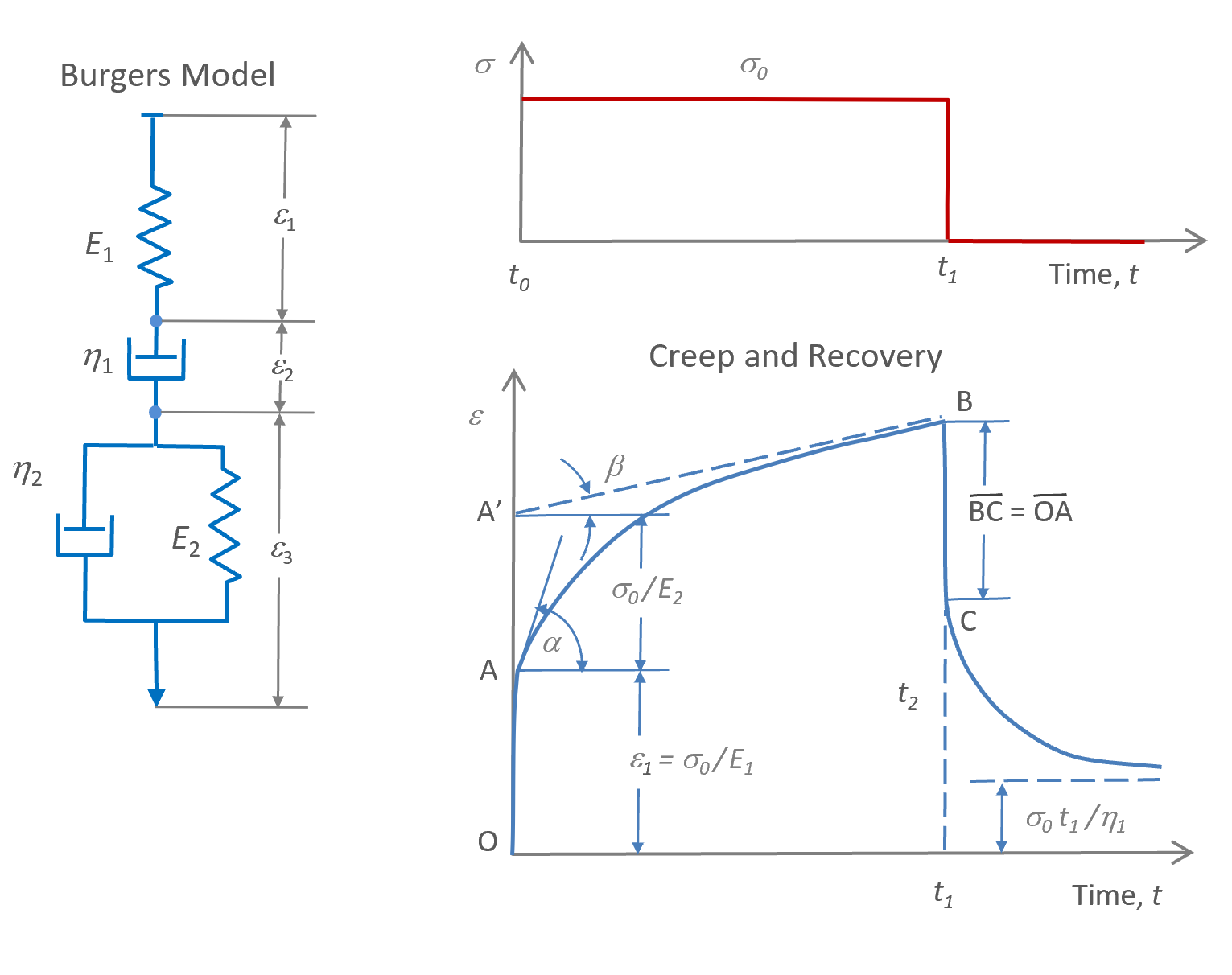
In the Burgers model, the spring of the Maxwell element represents the instantaneous elastic strain and its dashpot the non-reversible viscous flow, whereas the Voigt element describes the delayed elasticity. The total strain at constant stress is the sum of the strain in the three elements:

ε(t) = ε1 + ε2 + ε3

Where ε1 is the strain in the spring, ε2 is the strain in the dashpot and ε3 is the strain in the Voigt element. In the case of constant creep the solution of this equation is found to be

ε(t) = σ0 / E2 · [1 - σ0 e- t/τ] + σ0 / E1 + σ0 / η1 · t

The equation above has four unknowns which can he determined from the creep curve and from following initial conditions at t = 0:

ε(t=0) = ε1 = σ0 / E1
ε2 = ε3 = 0

where σ0 / E1 is the initial jump in strain which is caused by the spring 1. The creep rate at the start t = 0 can be found by differentiating the strain equation of the Burgers model:

dε / dt = σ0 / η1 + σ0 / η2 · e-t/τ

where τ = η2/E2 is the response time of the one-dimensional Voigt element. Then the strain rate (creep rate) at t = 0 reads

dε / dt|0= σ0 / η1 + σ0 / η2 = tan α

where tan α is the initial slope at t = 0. For very large t → ∞, the creep rate reaches asymptotically the value

dε / dt|∞= σ0 / η1 = tan β

Note, many thermoplastics have a continuously decreasing creep rate, so that the asymptote of the strain rate is zero. Nevertheless, the creep of such a plastic may still be fitted to the Burgers model over a finite time span.

Notes & Further Readings
  1. A material is considered linearly viscoelastic if stress is proportional to strain at a given time and if the linear superposition principle is applicable.
  2. Retardation is the delayed response to an applied (constant) stress whereas stress relaxation is a gradual reduction in stress with time at constant strain.
  3. F. Mainardi and G. Spada, Eur. Phys. J., Spec. Topics, 193(1), pp 133-160 (2011)
  4. W.N. Findley, J.S. Lai, & K. Onaran, Creep and Relaxation of Nonlinear Viscoelastic Materials, North-Holland Publ. Comp., Oxford 1976
  5. D. Roylance, Engineering Viscoelasticity, Dept. Mat. Sci. & Engrg., MIT, 2001
  6. Rois bert O. Ebewele, Polymer Science and Technology, CRC Press, Boca Raton, Florida 2000
  7. A.D. Drozdov, Viscoelastic Structures. Academic Press, New York, 1998
  8. L.H. Sperling, Introduction to Physical Polymer Science, New York, 1992

August 27, 2020

  • Summary

    Viscoelastic Materials

    At short time scales, solid polymers under stress behave like elastic materials, whereas at large time scales, they will undergo viscous flow and disentanglement.

  • Knowledge of the viscoelastic response is a prerequisite for designing and optimizing structural plastic parts and structural bonds that are subjected to stress.

  • The viscoelastic behavior of plastics and rubbers can be captured by an arrangement of dashpots and springs that describe the viscoelastic response to an applied stress or strain.

  • The simplest models that capture both the relaxation and retardation are the so-called standard linear solid models, also known as three-parameter models.

  • These models are obtained by adding a spring either in series to a Voigt (Kelvin) model or in parallel to a Maxwell model.

  • While some problems in viscoelasticity can be solved with three-parameter models, more often Voigt and Maxwell elements are combined to more complex arrangements.

  • The simplest model that exhibits all the important features of visco-elasticity is the so-called four-element model, also known as the Burgers model. It is obtained by adding a Voigt element in series to a Maxwell model.

  • In the Burgers model, the spring of the Maxwell element represents the instantaneous elastic strain and its dashpot the non-reversible viscous flow, whereas the Voigt element describes the delayed elasticity.